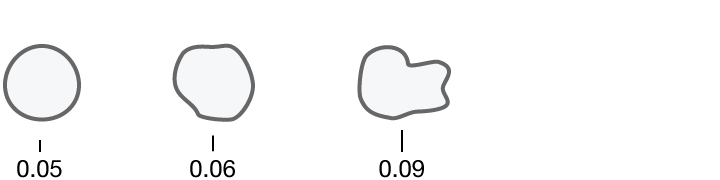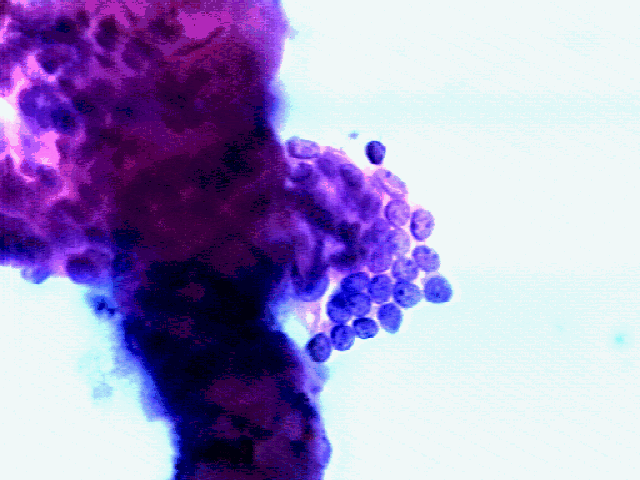
What humans see
Under a microscope, cancer looks "primitive and aggressive," a chaotic agglomeration of cells with irregularly shaped, sized, and patterned nuclei.
What computers "see"
Researchers quantified ten characteristics of cell nuclei in breast-cancer biopsy images.
Radius
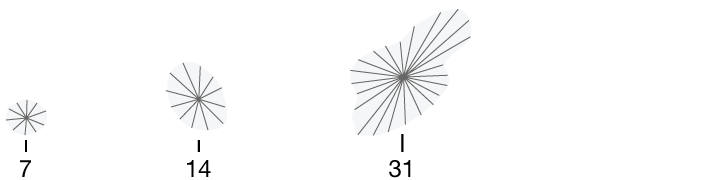
Perimeter
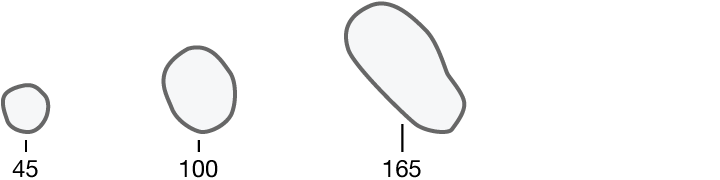
Area
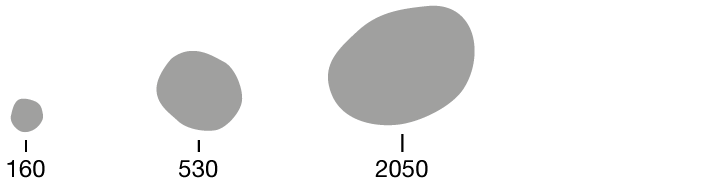
Texture

Smoothness
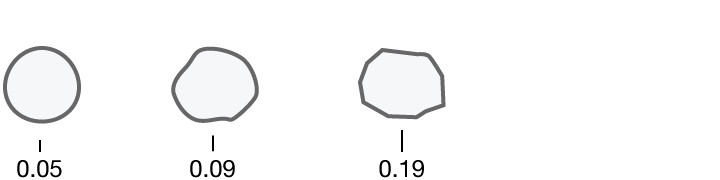
Compactness
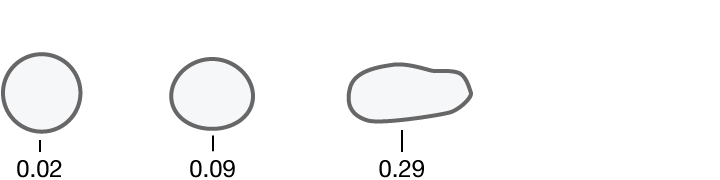
Concavity
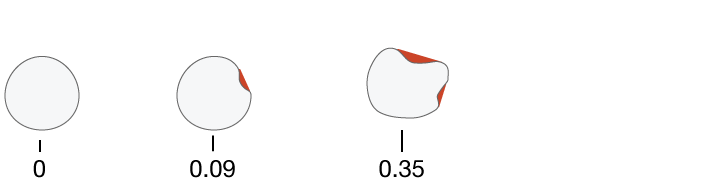
Concave Points
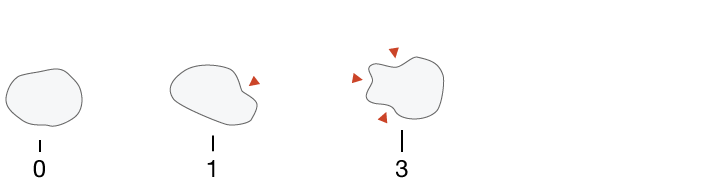
Symmetry
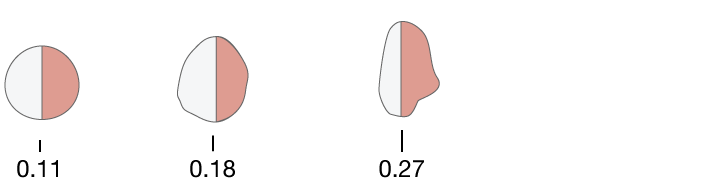
Fractal Dimensions